Classical Mechanics Notes

Date: 2024/05/23
Last Updated: 2024-05-25T20:04:46.000Z
Categories: Physics
Tags: Physics, Classical Mechanics
Read Time: 17 minutes

0.1 Contents

0.2 Kinematics
0.3 Forces
0.4 Work and Energy
0.5 Lagrangian Mechanics
0.6 Small Oscillations
0.7 Normal Modes
0.8 Hamiltonian Mechanics

Given a particle of mass and position vector $\mathbf{r}$ , the second law states that the force $\mathbf{F}$ acting on the particle is equal to the time derivative of the momentum $\mathbf{p}$ of the particle:

$\mathbf{F} = \frac{d\mathbf{p}}{dt}$

If the mass of the particle is constant, then the second law can be written in terms of the acceleration $\mathbf{a}$ of the particle:

$\mathbf{F} = m\mathbf{a}$

0.2.2 Inertial Frames and Galileo Transformation

Given a frame of reference $\mathbf{S}$ and another frame of reference $\mathbf{S}'$ moving with equation of motion $\mathbf{s} = \mathbf{s}(t)$ with respect to $\mathbf{S}$ , and rotation with respect to $\mathbf{S}$ with orthogonal matrix $\mathbf{O}(t)$ , the transformation of the position vector $\mathbf{r}'$ in $\mathbf{S}'$ to $\mathbf{r}$ in $\mathbf{S}$ is given by:

$\mathbf{r} = O(t)\mathbf{r}' + \mathbf{s}(t)$

And the transformation of the force $\mathbf{F}'$ in $\mathbf{S}'$ to $\mathbf{F}$ in $\mathbf{S}$ is given by:

$\mathbf{F} = \mathbf{O}(t)\mathbf{F}'$

Assume in $\mathbf{S}$ , the second law holds, then in $\mathbf{S}'$ :

$m\ddot{\mathbf{r}} = \ddot{\mathbf{O}}\mathbf{r'} + 2\dot{\mathbf{O}}\dot{\mathbf{r}'} + \ddot{\mathbf{r}'}\mathbf{O} + \ddot{\mathbf{s}} = \mathbf{F} \neq \mathbf{O}(t)\mathbf{F}'$

However, if $\mathbf{O}$ is a constant orthogonal matrix, and $\mathbf{s}$ is a linear function of time, then the second law holds in $\mathbf{S}'$ . Such frames are called inertial frames. And the corresponding transformation is called Galileo transformation.

0.2.3 Momentum Conservation

Given a system of particles, the total momentum $\mathbf{P}$ of the system is given by:

$\mathbf{P} = \sum_i \mathbf{p}_i$

If the net external force acting on the system is zero, then the total momentum of the system is conserved:

$\frac{d\mathbf{P}}{dt} = \sum_i \frac{d\mathbf{p}_i}{dt} = \sum_i \mathbf{F}_i = \mathbf{F}_{\text{ext}} = 0$

0.2.3.1 Momentum Conservation in specific directions

Given a constant vector $\mathbf{a}$ , if the net external force acting on the system is zero in the direction of $\mathbf{a}$ , then the total momentum of the system in the direction of $\mathbf{a}$ is conserved:

$\frac{d}{dt}\left(\sum_i \mathbf{p}_i\cdot\mathbf{a}\right) = \sum_i \mathbf{F}_i\cdot\mathbf{a} = \mathbf{F}_{\text{ext}}\cdot\mathbf{a} = 0$

0.2.4 Angular Momentum

Given a particle of mass and position vector $\mathbf{r}$ , the angular momentum $\mathbf{L}$ of the particle with respect to the origin is given by:

$\mathbf{L} = \mathbf{r}\times\mathbf{p}$

0.2.5 Torque (Moment of Force)

Given a particle of mass and position vector $\mathbf{r}$ , and a force $\mathbf{F}$ acting on the particle, the torque $\mathbf{\tau}$ of the particle with respect to the origin is given by:

$\mathbf{\tau} = \mathbf{r}\times\mathbf{F}$

The torque represent the tendency of the force to rotate the particle.

0.2.5.1 Torque and Angular Momentum

Given a particle of mass and position vector $\mathbf{r}$ , and a force $\mathbf{F}$ acting on the particle, the time derivative of the angular momentum $\mathbf{L}$ of the particle with respect to the origin is given by:

$\frac{d\mathbf{L}}{dt} = \mathbf{r}\times\mathbf{F} = \mathbf{\tau}$

0.2.6 Angular Momentum Conservation

Given a system of particles, the total angular momentum $\mathbf{L}$ of the system with respect to the origin is given by:

$\mathbf{L} = \sum_i \mathbf{L}_i = \sum_i \mathbf{r}_i\times\mathbf{p}_i$

If the net external torque acting on the system is zero, then the total angular momentum of the system is conserved:

$\frac{d\mathbf{L}}{dt} = \sum_i \frac{d\mathbf{L}_i}{dt} = \sum_i \mathbf{\tau}_i = \mathbf{\tau}_{\text{ext}} = 0$

0.2.6.1 Angular momentum conservation in specific directions

Given a constant vector $\mathbf{a}$ , if the net external torque acting on the system is zero in the direction of $\mathbf{a}$ , then the total angular momentum of the system in the direction of $\mathbf{a}$ is conserved:

$\frac{d}{dt}\left(\sum_i \mathbf{L}_i\cdot\mathbf{a}\right) = \sum_i \mathbf{\tau}_i\cdot\mathbf{a} = \mathbf{\tau}_{\text{ext}}\cdot\mathbf{a} = 0$

0.3 Forces

0.3.1 Newton's Third Law

Given two particles and with forces $\mathbf{F}_{ij}$ and $\mathbf{F}_{ji}$ acting on them, the third law states that the forces are equal in magnitude and opposite in direction:

$\mathbf{F}_{ij} = -\mathbf{F}_{ji}$

0.3.2 Gravity

Given two particles and with masses m_i and m_j and position vectors $\mathbf{r}_i$ and $\mathbf{r}_j$ ,

the gravitational force $\mathbf{F}_{ij}$ acting on particle due to particle is given by:

$\mathbf{F}_{ij} = -\frac{Gm_im_j}{|\mathbf{r}_i - \mathbf{r}_j|^3}(\mathbf{r}_i - \mathbf{r}_j)$

where is the gravitational constant.

0.3.2.1 The Gravitational Constant

The gravitational constant is a fundamental constant in physics. It is defined as the constant of proportionality in Newton's law of universal gravitation:

$\mathbf{F} = -\frac{Gm_1m_2}{r^2}\hat{\mathbf{r}}$

where $\mathbf{F}$ is the force between two point masses m_1 and m_2 separated by a distance , and $\hat{\mathbf{r}}$ is the unit vector pointing from m_1 to m_2 .

The value of is approximately $6.67430\times10^{-11}\,\text{m}^3\,\text{kg}^{-1}\,\text{s}^{-2}$ .

0.3.2.2 Near Earth's Surface

Given a particle of mass near the surface of the Earth with acceleration due to gravity , the gravitational force $\mathbf{F}_g$ acting on the particle is given by:

$\mathbf{F}_g = --\frac{Gm_1m_2}{r^2}\hat{\mathbf{r}}$

where m_1 is the mass of the Earth, m_2 is the mass of the particle, and is the distance between the particle and the center of the Earth.

As the particle is near the surface of the Earth, the distance is approximately the radius of the Earth . And the mass of the Earth is a constant m_1 = M .

Therefore, the gravitational force $\mathbf{F}_g$ acting on the particle is given by:

$\mathbf{F}_g = -\frac{GMm}{R^2}\hat{\mathbf{r}}$

where is the mass of the Earth.

Given the acceleration due to gravity $g = \frac{GM}{R^2}$ , the gravitational force $\mathbf{F}_g$ acting on the particle is given by:

$\mathbf{F}_g = -mg\hat{\mathbf{r}}$

where is the acceleration due to gravity. The common value of is approximately $9.81\,\text{m/s}^2$ .

0.3.3 Elastic Forces

The forces due to the tendency of a object to restore its original shape are called elastic forces.

0.3.3.1 Hooke's Law

Given a spring with spring constant and displacement , the elastic force acting on the spring is given by:

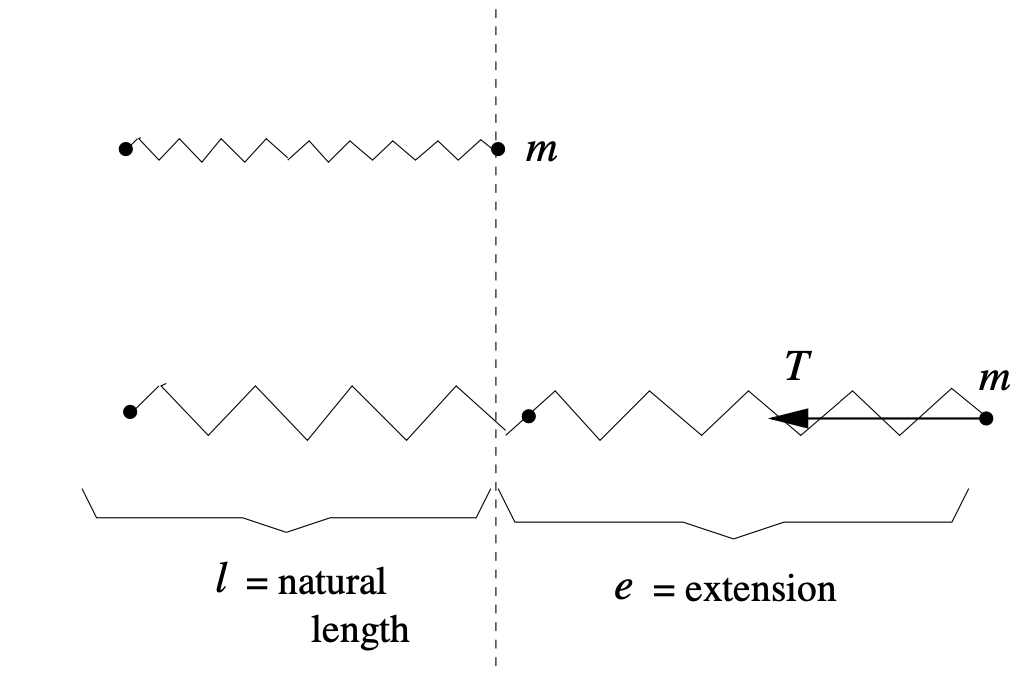
Hooke's Law

0.3.4 Contact Forces

The forces due to the contact of two objects are called contact forces.

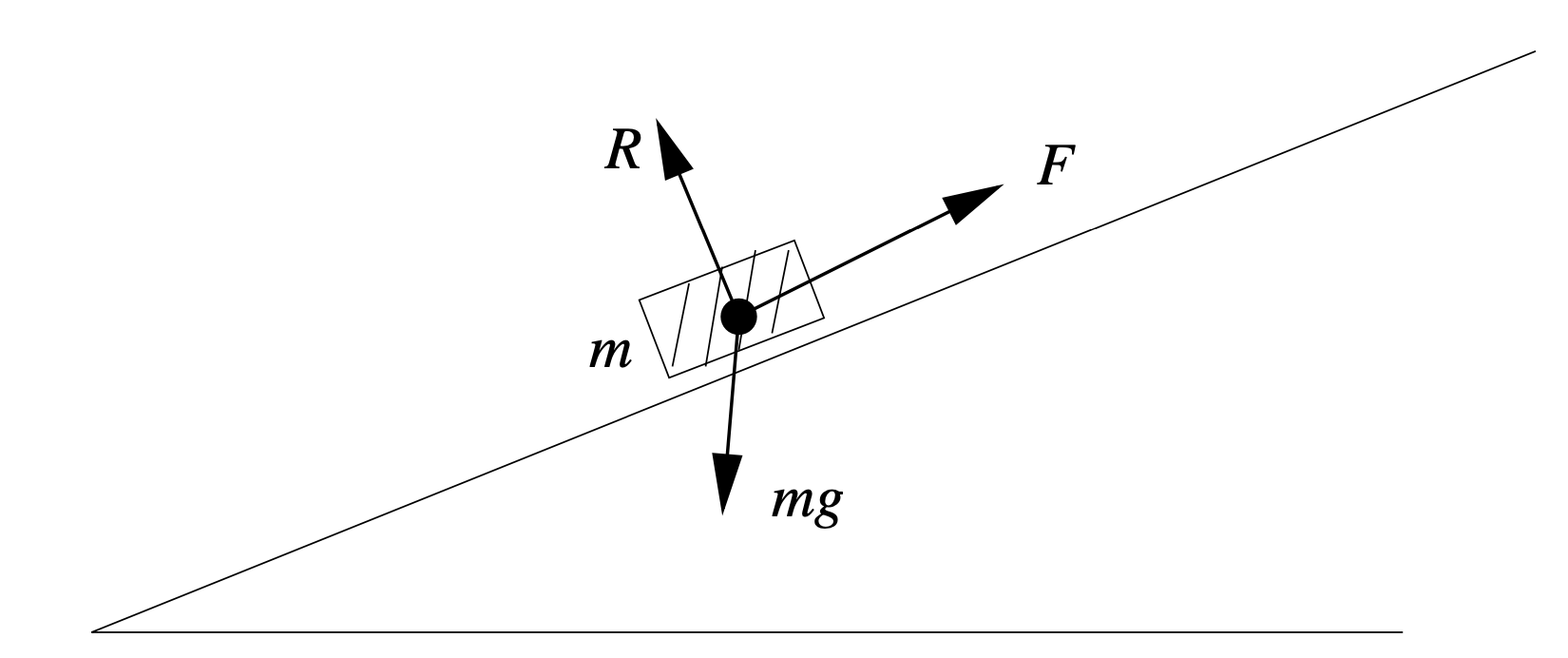
Contact Forces

Where is the normal force, is the frictional force.

0.3.4.1 Moving Friction

Given a moving object on a surface with coefficient of kinetic friction $\mu_k$ , and normal force acting on the object, the frictional force F_k acting on the object is given by:

$F_k = -\mu_k R$

0.4 Work and Energy

0.4.1 Potential Energy

Given a particle of mass and position vector $\mathbf{r}$ , the potential energy of the particle is given by:

$U = U(\mathbf{r})$

and the force $\mathbf{F}$ acting on the particle is given by:

$\mathbf{F} = -\nabla U$

Consequently, the potential energy can be expressed in terms of the force $\mathbf{F}$ acting on the particle:

$U = -\int \mathbf{F}\cdot d\mathbf{r}$

0.4.2 Energy Conservation

Given a particle of mass and position vector $\mathbf{r}$ , the total energy of the particle is given by:

where is the kinetic energy of the particle, and is the potential energy of the particle.

If the net external force acting on the particle is zero, then the total energy of the particle is conserved:

$\begin{align} \frac{dE}{dt} &= \frac{dT}{dt} + \frac{dU}{dt} \\ &= \frac{d}{dt}\left(\frac{1}{2}mv\cdot v\right) -\nabla U \frac{d\mathbf{r}}{dt} \\ &= \frac{d}{dt}\left(\frac{1}{2}mv^2\right) -\nabla U \cdot \mathbf{v} \\ &= m\mathbf{v}\cdot\mathbf{a} - \mathbf{F}\cdot\mathbf{v} \\ &= \mathbf{F}\cdot\mathbf{v} - \mathbf{F}\cdot\mathbf{v} \\ &= 0 \end{align}$

0.4.2.1 Conservative Forces

Given a force $\mathbf{F}$ acting on a particle, if the force is conservative, then the force can be expressed as the gradient of a scalar function:

$\mathbf{F} = -\nabla U$

where is the potential energy of the particle.

For conservative forces, on a simply connected domain (the domain is path connected and any closed curve can be shrunk to a point without leaving the domain), the work done by the force $\mathbf{F}$ on the particle is path independent:

$\int_{\mathbf{r}_1}^{\mathbf{r}_2} \mathbf{F}\cdot d\mathbf{r} = U(\mathbf{r}_1) - U(\mathbf{r}_2)$

0.4.2.1.1 Example: Non-conservative Forces

Given a force $\mathbf{F}$ acting on a particle, where the force can be expressed as:

$\mathbf{F}(x,y,z) = (0,0,x)$

by solving the PDE, there is no potential energy such that:

$\mathbf{F} = -\nabla U$

Thus, the force $\mathbf{F}$ is non-conservative.

0.4.2.1.2 Essential Conditions for Conservative Forces

Given a force $\mathbf{F}$ acting on a particle, the force is conservative if the following conditions are satisfied:

The force $\mathbf{F}$ is a function of the position vector $\mathbf{r}$ only.
The force $\mathbf{F}$ is irrotational, that is, the curl of the force is zero:
$\nabla\times\mathbf{F} = 0$

0.4.2.2 Qualitative Energy Analysis

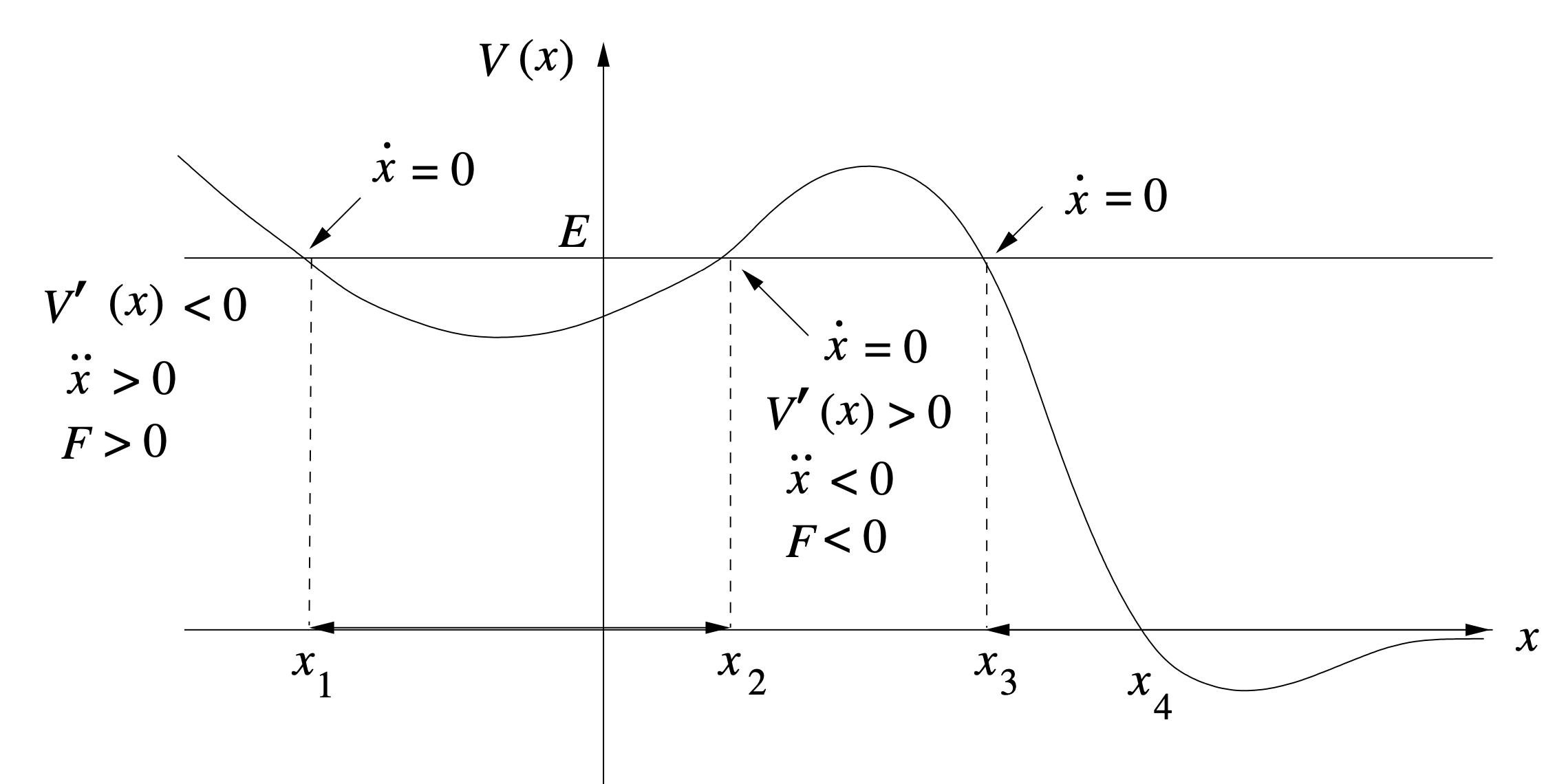
Energy Analysis

At point $x_{1}$ , the particle has speed $\dot{x} = 0$ and potential energy V'(x) < 0 . Thus, the particle has to move to the right.

At point $x_{2}$ , the particle has speed $\dot{x} = 0$ and potential energy V'(x) > 0 . Thus, the particle has to move to the left.

If the initial position of the particle is inside $[x_{1},x_{2}]$ , then the particle will oscillate between $x_{1}$ and $x_{2}$ . As it can not go beyond $x_{1}$ and $x_{2}$ .

As when $x \rightarrow \infty$ , the potential energy $V(x) \rightarrow 0$ , the speed of the particle $\dot{x} \rightarrow \sqrt{\frac{2E}{m}}$ .

0.4.3 Work

Given a particle of mass and position vector $\mathbf{r}$ , the work done by a force $\mathbf{F}$ on the particle along a path is given by:

$W = \int_C \mathbf{F}\cdot d\mathbf{r}$

0.4.3.1 Work and Kinetic Energy

Given a particle of mass and position vector $\mathbf{r}$ , the work done by a force $\mathbf{F}$ on the particle is equal to the change in kinetic energy of the particle:

$T(t_{1}) - T(t_{0}) = W = \int_{t_{0}}^{t_{1}} \mathbf{F}\cdot\mathbf{v} dt$

0.5 Lagrangian Mechanics

If we are working with some coordinate that are not Cartesian (e.g. Polar Coordinate), we can use the Lagrangian mechanics to describe the motion of the system.

0.5.1 Lagrangian

Given a system of particles with generalized coordinates q_i , as the system evolves in time, which means the generalized coordinates q_i are functions of time , we are also given $\dot{q}_{i}$ .

The Lagrangian of the system is given by:

where is the kinetic energy of the system, and is the potential energy of the system, and both are functions of the generalized coordinates q_i and their time derivatives $\dot{q}_{i}$ and possibly time .

0.5.2 Euler-Lagrange Equation

Given a system of particles with generalized coordinates q_i , the Euler-Lagrange equation is given by:

$\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{q}_{i}}\right) - \frac{\partial L}{\partial q_{i}} = 0$

0.5.3 Action Integral

Given a system of particles with generalized coordinates q_i , the action integral of the system is given by:

$S[q] = \int_{t_{0}}^{t_{1}} L(q,\dot{q},t) dt$

0.5.4 Hamilton's Principle

The solution to the Euler-Lagrange equation is the path q(t) that is a stationary point of the action integral S[q] .

0.5.5 Geodesic Equation

Given a arbitrary manifold. Given two point and on the manifold, and a curve $\gamma$ connecting and .

If the length of the curve $\gamma$ is given by the integral:

$L[\gamma] = \int_{0}^{1} g(\gamma) dt$

for some function .

And we wish to find the curve $\gamma$ that minimizes the length $L[\gamma]$ .

The curve $\gamma$ that minimizes the length $L[\gamma]$ is called the geodesic.

If we define the Lagrangian as:

$L = g(\gamma,\dot{\gamma})$

Then the Euler-Lagrange equation is the geodesic equation.

0.5.6 Generalised Coordinates in Lagrangian Mechanics

Given a system of particles with generalized coordinates q_i .

The velocity of the particle is given by:

$\mathbf{v} = \sum_i \dot{q}_{i}$

The momentum of the particle is given by:

$\mathbf{p} = \sum_i \frac{\partial L}{\partial \dot{q}_{i}}$

The force acting on the particle is given by:

$\mathbf{F} = \sum_i \frac{\partial L}{\partial q_{i}}$

0.5.6.1 Cyclical Coordinates

Given a system of particles with generalized coordinates q_i , if the Lagrangian does not depend on a generalized coordinate q_i , then the generalized coordinate q_i is called a cyclical coordinate.

If the Lagrangian does not depend on a cyclical coordinate q_i , then the momentum $\frac{\partial L}{\partial \dot{q}_{i}}$ is conserved. Which means $\frac{\partial L}{\partial \dot{q}_{i}}$ is a constant.

0.5.7 Example: Central Force

Given a particle of mass moving in a plane with polar coordinates $(r,\theta)$ , with potential energy U(r) that depends only on the distance from the origin,

As, the potential is independent of the angle $\theta$ , the force acting on the particle is radial.

The Lagrangian of the particle is given by:

$L = \frac{1}{2}m\left(\dot{r}^2 + r^2\dot{\theta}^2\right) - U(r)$

The Euler-Lagrange equation for the angular coordinate $\theta$ is given by:

$\begin{align} \frac{d}{dt}\left(\frac{\partial L}{\partial \dot{\theta}}\right) - \frac{\partial L}{\partial \theta} &= 0 \\ \frac{d}{dt}\left(mr^2\dot{\theta}\right) &= 0 \\ mr^2 \dot{\theta} = J \end{align}$

We usually call the angular momentum of the particle. And in the central force situation the angular momentum is conserved.

The Euler-Lagrange equation for the radial coordinate is given by:

$\begin{align} \frac{d}{dt}\left(\frac{\partial L}{\partial \dot{r}}\right) - \frac{\partial L}{\partial r} &= 0 \\ \frac{d}{dt}\left(m\dot{r}\right) - m\dot{\theta}^2r &= -\frac{dU}{dr} \\ m\ddot{r} - m\dot{\theta}^2r &= -\frac{dU}{dr} \\ m\ddot{r} &= \frac{J^2}{mr^3} -\frac{dU}{dr} \end{align}$

The energy of the particle is given by:

$E = \frac{1}{2}m\left(\dot{r}^2 + r^2\dot{\theta}^2\right) + U(r)$

And as:

$\begin{align} \frac{dE}{dt} &= \frac{d}{dt}\left(\frac{1}{2}m\dot{r}^2 + \frac{1}{2}mr^2\dot{\theta}^2 + U(r)\right) \\ &= \frac{d}{dt}\left(\frac{1}{2}m\dot{r}^2 + \frac{1}{2}\frac{J^2}{mr^2} + U(r)\right) \\ &= m\dot{r}\ddot{r} - \frac{J^2}{mr^3}\dot{r} + \frac{dU}{dr}\dot{r} \\ &= 0 \end{align}$

The energy of the particle is conserved. And we usually call the total energy of the particle. And also the effective potential:

$U_{\text{eff}}(r) = U(r) + \frac{J^2}{2mr^2}$

If we are give the effective potential $U_{\text{eff}}(r)$ , the energy and angular momentum of the particle, then the equation of motion of the particle can be determined by solving two first order ODEs:

$\begin{align} E_{0} &= \frac{1}{2}m\dot{r}^2 + U_{\text{eff}}(r) \\ J &= mr^2\dot{\theta} \end{align}$

0.5.8 Lagrangian Mechanics with Constraints

0.5.8.1 Holonomic Constraints

Given a system of particles with generalized coordinates q_i , if the generalized coordinates q_i are subject to constraints $f(q_1,\dots,q_i,t) = 0$ , then the constraints are called holonomic constraints.

Any constraints that can not be expressed in the form $f(q_1,\dots,q_i,t) = 0$ are called non-holonomic constraints.

Example: Object with air resistance is a non-holonomic constraint, as the air resistance is independent of the speed of the object.

0.5.8.1.1 Unforced or Natural Constraints

Given a system of particles with generalized coordinates q_i , if the constraints f_j(q_i,t) = 0 are independent of the time , then the constraints are called unforced or natural constraints.

Example: A particle moving on a sphere of radius .

Example: A pendulum with fixed suspension point.

0.5.8.1.2 Forced Constraints

Given a system of particles with generalized coordinates q_i , if the constraints f_j(q_i,t) = 0 are dependent of the time , then the constraints are called forced constraints.

Example: A particle moving on a sphere of radius with the sphere rotating.

Example: A pendulum with the suspension point moving.

0.5.9 System of Particles and Rigid Bodies

0.5.9.1 Centre of Mass

Given a system of particles with masses m_i and position vectors $\mathbf{r}_i$ , the centre of mass $\mathbf{R}$ of the system is given by:

$\mathbf{R} = \frac{\sum_i m_i\mathbf{r}_i}{\sum_i m_i}$

0.5.9.2 Total Momentum

Given a system of particles with masses m_i and position vectors $\mathbf{r}_i$ , the total momentum $\mathbf{P}$ of the system is given by:

$\begin{align} \mathbf{P} &= \sum_i \mathbf{p}_i \\ &= \sum_i m_i\mathbf{v}_i \\ &= \sum_i m_i\dot{\mathbf{r}}_i \\ &= \dot{\sum_i m_i{\mathbf{r}}_i} \\ &= \dot{\mathbf{R}} \sum_i m_i \\ \end{align}$

0.5.9.3 Total Angular Momentum

Given a system of particles with masses m_i and position vectors $\mathbf{r}_i$ , the total angular momentum $\mathbf{L}$ of the system with respect to the origin is given by:

$\begin{align} \mathbf{L} &= \sum_i \mathbf{L}_i \\ &= \mathbf{R} \times \mathbf{P} + \sum_i (\mathbf{r}_i - \mathbf{R})\times (\mathbf{p}_i - \mathbf{P})\\ \end{align}$

The term $\sum_i (\mathbf{r}_i - \mathbf{R})\times (\mathbf{p}_i - \mathbf{P})$ is the angular momentum of the system with respect to the centre of mass.

0.5.9.4 Total Kinetic Energy

Given a system of particles with masses m_i and position vectors $\mathbf{r}_i$ , and the total mass of the system , the total kinetic energy of the system is given by:

$\begin{align} T &= \sum_i T_i \\ &= \sum_i \frac{1}{2}m_i\mathbf{v}_i\cdot\mathbf{v}_i \\ &= \frac{1}{2} M \dot{\mathbf{R}}^2 + \sum_i \frac{1}{2}m_i(\dot{\mathbf{r}}_i - \dot{\mathbf{R}})^2 \\ \end{align}$

The term $\sum_i \frac{1}{2}m_i(\dot{\mathbf{r}}_i - \dot{\mathbf{R}})^2$ is the kinetic energy of the system with respect to the centre of mass.

0.5.9.5 Separable Potential Energy

Given a system of particles with masses m_i and position vectors $\mathbf{r}_i$ , and the total mass of the system , the total potential energy of the system is given by:

$\begin{align} U &= \sum_i U_i \\ &= \sum_i U_i(\mathbf{r}_i) \end{align}$

If the potential energy is separable, that is, the potential energy can be expressed as:

$U = U_{\mathbf{R}}(\mathbf{R}) + \sum_i U_i(\mathbf{r}_i)$

Then the generalised coordinates q_i can be reformulated using the center of mass $\mathbf{R}$ and the relative coordinates $\mathbf{r}_i - \mathbf{R}$ . And the Lagrangian can be expressed in terms of the center of mass $\mathbf{R}$ and the relative coordinates $\mathbf{r}_i - \mathbf{R}$ .

$\begin{align} L_{0} &= T_{0} - U_{0} = \frac{1}{2}M\dot{\mathbf{R}}^2 - U_{\mathbf{R}}(\mathbf{R}) \\ L_{i} &= T_{i} - U_{i} = \frac{1}{2}m_i(\dot{\mathbf{r}}_i - \dot{\mathbf{R}})^2 - U_i(\mathbf{r}_i-\mathbf{R}) \end{align}$

Example: A constant gravitational field acting on a system of particles is a separable potential energy. And the total potential energy of the system is given by: $U = U_{\mathbf{R}}(\mathbf{R})$ , which only depend on the center of mass $\mathbf{R}$ .

0.5.9.5.1 Example: Two Particles

Given two particles and with masses m_1 and m_2 and position vectors $\mathbf{r}_1$ and $\mathbf{r}_2$ ,

Then let:

$\begin{align} \mathbf{R} &= \frac{m_1\mathbf{r}_1 + m_2\mathbf{r}_2}{m_1 + m_2} \\ \mathbf{r} &= \mathbf{r}_2 - \mathbf{r}_1 \end{align}$

Thus,

$\begin{align} \mathbf{r}_1 &= \mathbf{R} - \frac{m_2}{m_1 + m_2}\mathbf{r} \\ \mathbf{r}_2 &= \mathbf{R} + \frac{m_1}{m_1 + m_2}\mathbf{r} \end{align}$

The kinetic energy of the system is given by:

$\begin{align} T &= \frac{1}{2}M\dot{\mathbf{R}}^2 + \left[\frac{1}{2}m_{1}(\dot{\mathbf{r}}_{2}-\dot{\mathbf{R}})^2 + \frac{1}{2}m_{2}(\dot{\mathbf{r}}_{2}-\dot{\mathbf{R}})^2 \right] \\ &= \frac{1}{2}M\dot{\mathbf{R}}^2 + \frac{1}{2}\frac{m_1m_2}{m_1+m_2}\dot{\mathbf{r}}^2 \end{align}$

And the potential is given by:

$U = U_{\mathbf{r}}(\mathbf{r})$

Thus, the Lagrangian of the system is given by:

$L = \frac{1}{2}M\dot{\mathbf{R}}^2 + \frac{1}{2}\frac{m_1m_2}{m_1+m_2}\dot{\mathbf{r}}^2 - U_{\mathbf{r}}(\mathbf{r})$

Apparently, the Lagrangian is cyclic in $\mathbf{R}$ . Thus, the total momentum $\mathbf{P}$ of the system is conserved.

0.5.9.6 Rigid Bodies

A rigid body is a system of particles with fixed relative distances between the particles.

For rigid body, we use $\mathbf{R}$ to denote the position of the center of mass of the rigid body, and $\mathbf{\rho}_i= (\rho_i, \varphi_i)$ in polar coordinates to denote the position of the -th particle with respect to the center of mass.

As, the relative distances between the particles are fixed, $\rho_i$ is a constant of time. And also, the angular velocity $\dot{\varphi}_i$ is the same for all particles, in convention, we use $\dot{\varphi}_i = \varphi$ to denote the angular velocity of the rigid body.

0.5.9.6.1 Moment of Inertia

Given a rigid body with mass and position vector $\mathbf{R}$ , and the -th particle with mass m_i and position vector $\mathbf{\rho}_i$ , the kinetic energy of the rigid body is given by:

$\begin{align} T &= \frac{1}{2}M\dot{\mathbf{R}}^2 + \sum_i \frac{1}{2}m_i\dot{\mathbf{\rho}}_i^2 \\ &= \frac{1}{2}M\dot{\mathbf{R}}^2 + \sum_i \frac{1}{2}m_i(\rho_i^2\dot{\varphi}^2) \\ &= \frac{1}{2}M\dot{\mathbf{R}}^2 + \frac{1}{2} \dot{\varphi}^2 \sum_i m_i \rho_i^2 \end{align}$

The term $\sum_i m_i \rho_i^2$ is called the moment of inertia of the rigid body, which represents the resistance of the rigid body to rotation.

0.5.9.6.1.1 Example: The moment of inertia of a homogeneous disk

Given a homogeneous disk of radius and mass , the moment of inertia of the disk is given by:

$\begin{align} I &= \int_{0}^{2\pi} \int_{0}^{R} \rho^2 \rho \frac{M}{\pi R^2} d\rho d\varphi \\ &= \frac{M}{\pi R^2} \int_{0}^{2\pi} \int_{0}^{R} \rho^3 d\rho d\varphi \\ &= \frac{M}{\pi R^2} \int_{0}^{2\pi} \frac{1}{4}R^4 d\varphi \\ &= \frac{M}{\pi R^2} 2\pi \frac{1}{4}R^4 \\ &= \frac{1}{2}MR^2 \end{align}$

0.5.9.6.2 Example: Rolling Cylinder on an Inclined Plane

Consider the following system:

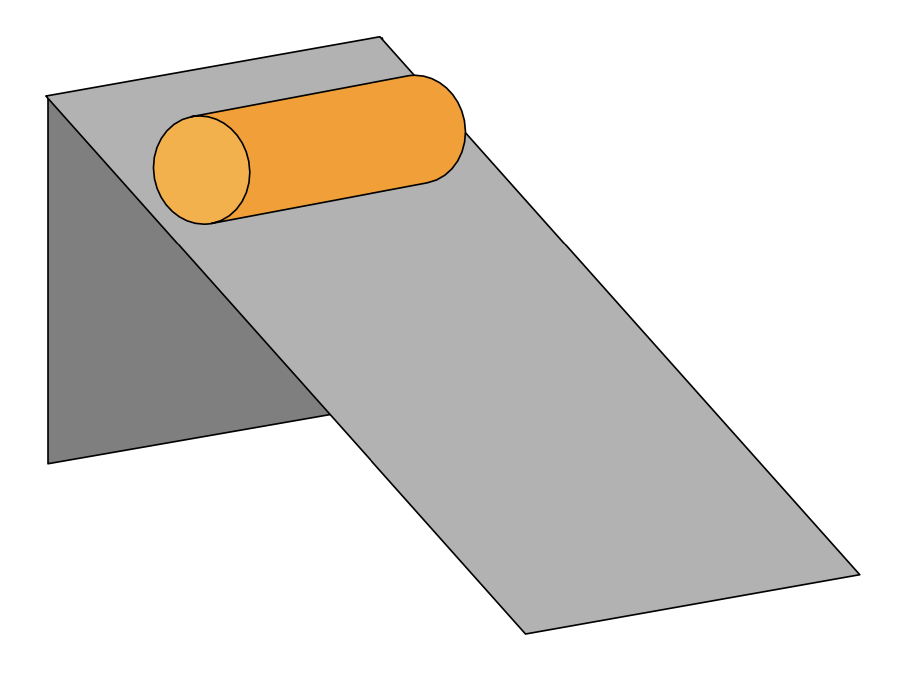
Rolling Cylinder

Given a cylinder of radius and mass rolling on an inclined plane with angle $\alpha$ , the question can be simplified by considering the following system:

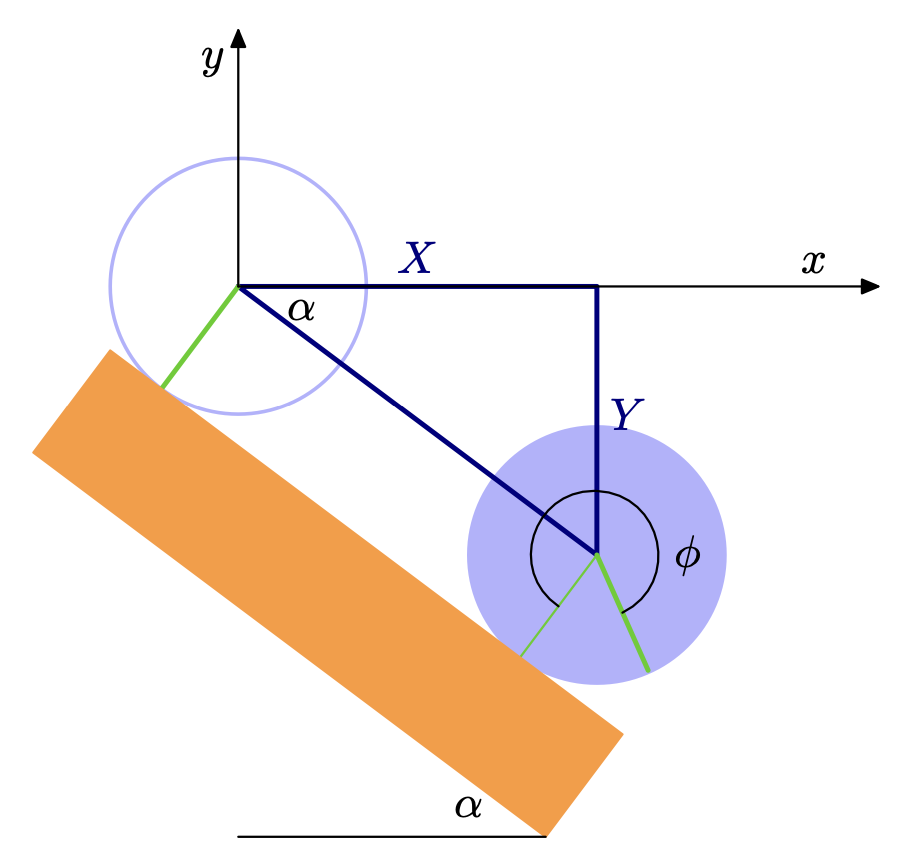
Rolling Cylinder Simplified

Where $\alpha$ is again the angle of the inclined plane, $\phi$ is the rolling angle of the cylinder, and R = (x,y) is the position of the center of mass of the cylinder.

As the cylinder is rolling on the plane with no sliding, we can formulate the constraints as:

$\begin{align} y &= -R\phi\sin(\alpha) \\ x &= R\phi\cos(\alpha) \end{align}$

Thus, the velocity of the center of mass of the cylinder is given by:

$\begin{align} \dot{R} &= (\dot{x},\dot{y}) \\ &= R\dot{\phi}(\cos(\alpha),-\sin(\alpha)) \end{align}$

And the kinetic energy of the cylinder is given by:

$\begin{align} T &= \frac{1}{2}M\dot{R}^2 + \frac{1}{2}I\dot{\phi}^2 \\ &= \frac{1}{2}M R^2 \dot{\phi}^2 + \frac{1}{2}I\dot{\phi}^2 \\ &= \frac{1}{2}M R^2 \dot{\phi}^2 + \frac{1}{2}I\dot{\phi}^2 \\ &= \frac{1}{2}M R^2 \dot{\phi}^2 + \frac{1}{4}M R^2 \dot{\phi}^2 \\ &= \frac{3}{4} M R^2 \dot{\phi}^2 \end{align}$

If we consider a constant gravitational field acting on the cylinder, the potential energy of the cylinder is given by:

$U = Mgy = -MgR\phi\sin(\alpha)$

The Lagrangian of the cylinder is given by:

$L = \frac{3}{4} M R^2 \dot{\phi}^2 + MgR\phi\sin(\alpha)$

Using the Euler-Lagrange equation, we can determine the equation of motion of the cylinder.

$\begin{align} \frac{d}{dt}\left(\frac{\partial L}{\partial \dot{\phi}}\right) - \frac{\partial L}{\partial \phi} &= 0 \\ \frac{d}{dt}\left(\frac{3}{2}M R^2 \dot{\phi}\right) - MgR\sin(\alpha) &= 0 \\ \frac{3}{2}M R^2 \ddot{\phi} - MgR\sin(\alpha) &= 0 \\ \ddot{\phi} &= \frac{2g\sin(\alpha)}{3R} \end{align}$

0.6 Small Oscillations

0.6.1 Harmonic Oscillator

Given a object with mass , spring constant , and displacement . The kinetic energy of the object is given by:

$T = \frac{1}{2}m\dot{x}^2$

The potential energy of the object is given by:

$U = \frac{1}{2}kx^2$

The Lagrangian of the object is given by:

$L = T - U = \frac{1}{2}m\dot{x}^2 - \frac{1}{2}kx^2$

By solving the Euler-Lagrange equation, we can determine the equation of motion of the object.

$\begin{align} \frac{d}{dt}\left(\frac{\partial L}{\partial \dot{x}}\right) - \frac{\partial L}{\partial x} &= 0 \\ \frac{d}{dt}\left(m\dot{x}\right) + kx &= 0 \\ m\ddot{x} + kx &= 0 \end{align}$

Thus,

$x = A \cos(\omega t + \phi), \omega = \sqrt{\frac{k}{m}}$

0.6.2 Small Oscillations in General

Given a system with generalized coordinates q_i , and potential energy of the system. And stationary points $q_{i0}$ of potential energy . Such that

$\frac{\partial U}{\partial q_i} = 0$

Then, the potential energy can be expanded as a Taylor series around the stationary points $q_{i0}$ .

$\begin{align} U &= U(q_{i0}) + \sum_i \frac{\partial U}{\partial q_i}(q_i - q_{i0}) + \frac{1}{2}\sum_{i,j} \frac{\partial^2 U}{\partial q_i \partial q_j}(q_i - q_{i0})(q_j - q_{j0}) + \cdots \\ &= U(q_{i0}) + \frac{1}{2}\sum_{i,j} \frac{\partial^2 U}{\partial q_i \partial q_j}(q_i - q_{i0})(q_j - q_{j0}) + \cdots \\ &\approx U(q_{i0}) + \frac{1}{2}\sum_{i,j} \frac{\partial^2 U}{\partial q_i \partial q_j}(q_i - q_{i0})(q_j - q_{j0}) \end{align}$

We could use symmetric matrix to represent the second order partial derivatives of the potential energy .

$K_{ij} = \frac{\partial^2 U}{\partial q_i \partial q_j}$

Thus, the potential energy can be expressed as:

$U = U(q_{i0}) + \frac{1}{2}(q-q_{0})^T K (q-q_{0})$

Also, in general, the kinetic energy of the system can be expressed using a positive definite symmetric matrix .

$T = \frac{1}{2}\dot{q}^T M \dot{q}$

Thus, in general, the Lagrangian of the system is given by:

$L = T - U = \frac{1}{2}\dot{q}^T M \dot{q} - U(q_{i0}) - \frac{1}{2}(q-q_{0})^T K (q-q_{0})$

0.6.3 Double Pendulum

Consider a double pendulum like below:

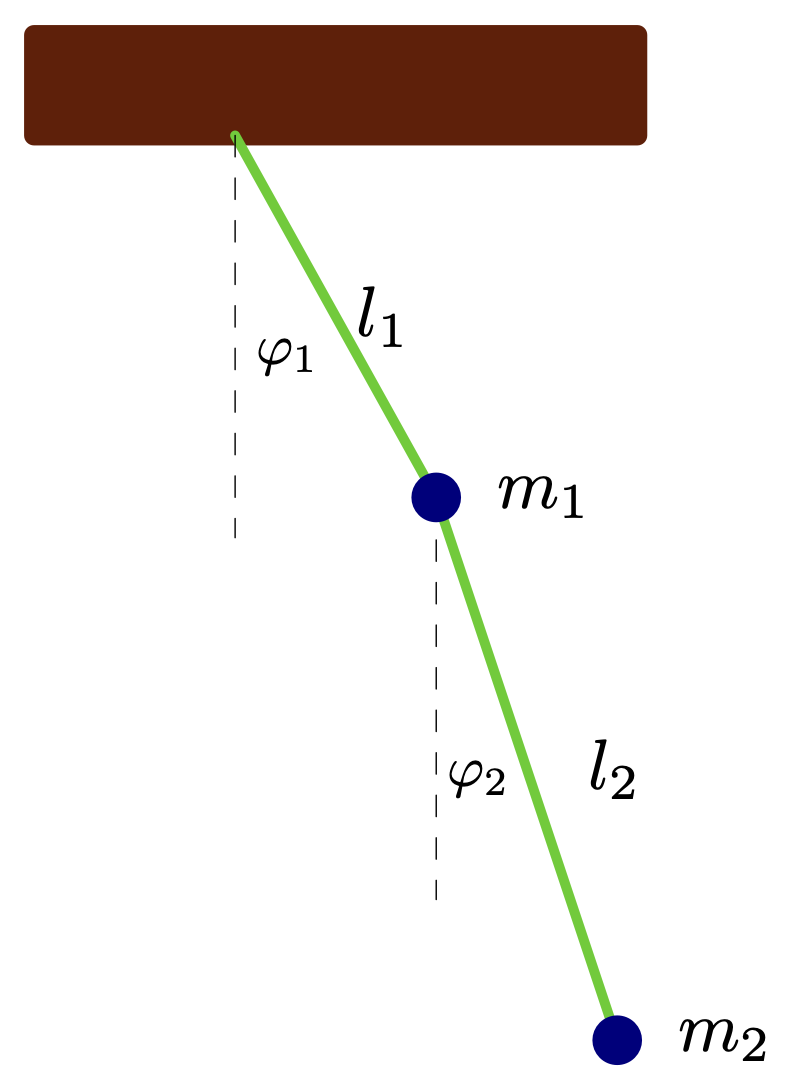
Double Pendulum

Thus, the stationary points of the double pendulum are given by:

$\begin{align} \varphi_1 &= 0 \\ \varphi_2 &= 0 \end{align}$

If we set the suspension point as the origin (0,0) , then the position of the first mass m_1 is given by:

$\begin{align} x_1 &= l_1\sin(\varphi_1) \\ y_1 &= -l_1\cos(\varphi_1) \end{align}$

And the position of the second mass m_2 is given by:

$\begin{align} x_2 &= l_1\sin(\varphi_1) + l_2\sin(\varphi_2) \\ y_2 &= -l_1\cos(\varphi_1) - l_2\cos(\varphi_2) \end{align}$

Thus, if we set $\varphi_1$ and $\varphi_2$ close to the stationary point, the kinetic energy of the double pendulum is given by:

$\begin{align} T &= \frac{1}{2}m_1\left(\dot{x}_1^2 + \dot{y}_1^2\right) + \frac{1}{2}m_2\left(\dot{x}_2^2 + \dot{y}_2^2\right) \\ &= \frac{1}{2}m_1\left(l_1^2\dot{\varphi}_1^2\right) + \frac{1}{2}m_2\left(l_1^2\dot{\varphi}_1^2 + l_2^2\dot{\varphi}_2^2 + 2l_1l_2\dot{\varphi}_1\dot{\varphi}_2\cos(\varphi_1 - \varphi_2)\right) \\ &\approx \frac{1}{2}m_1l_1^2\dot{\varphi}_1^2 + \frac{1}{2}m_2l_1^2\dot{\varphi}_1^2 + \frac{1}{2}m_2l_2^2\dot{\varphi}_2^2 + m_2l_1l_2\dot{\varphi}_1\dot{\varphi}_2 \end{align}$

The potential energy of the double pendulum is given by:

$\begin{align} U &= m_1gy_1 + m_2gy_2 \\ &= -m_1gl_1\cos(\varphi_1) - m_2gl_1\cos(\varphi_1) - m_2gl_2\cos(\varphi_2) \\ &\approx -(m_1gl_1 + m_2gl_1)(1-\frac{1}{2}\varphi_1^2) - m_2gl_2(1-\frac{1}{2}\varphi_2^2) \end{align}$

0.7 Normal Modes

As in Small Oscillations in General, we can express the kinetic and potential energy of the system in terms of symmetric matrices and :

$\begin{align} T &= \frac{1}{2}\dot{q}^T M \dot{q} \\ U &= \frac{1}{2}(q-q_{0})^T K (q-q_{0}) \end{align}$

Thus, the general momentum of the system is given by:

$p = \frac{\partial L}{\partial \dot{q}} = M\dot{q}$

And the generalised force of the system is given by:

$Q = \frac{\partial L}{\partial q} = K(q-q_{0})$

And the Euler-Lagrange equation is given by:

$\begin{align} \frac{d}{dt}\left(\frac{\partial L}{\partial \dot{q}}\right) - \frac{\partial L}{\partial q} &= 0 \\ \frac{d}{dt}\left(M\dot{q}\right) - K(q-q_{0}) &= 0 \\ M\ddot{q} + K(q-q_{0}) &= 0 \end{align}$

As, is a positive definite symmetric matrix, the inverse of exists.

Thus, the equation of motion of the system can be expressed as:

$\ddot{q} + M^{-1}K(q-q_{0}) = 0$

A normal mode of the system is a solution of the above equation of the form:

Where c(t) is a scalar function of time, and is a vector that is independent of time.

Substituting the normal mode solution into the equation of motion of the system:

$\begin{align} \ddot{q} + M^{-1}K(q-q_{0}) &= 0 \\ \ddot{c}(t)v + c(t)M^{-1}K(v) &= 0 \\ \frac{\ddot{c}}{c(t)} v + M^{-1}K(v) &= 0 \end{align}$

Thus, is an eigenvector of the matrix $M^{-1}K$ with eigenvalue $\omega^2$ , where $\omega$ is the angular frequency of the normal mode. And, c(t) is a solution of the following ODE:

$\ddot{c} + \omega^2 c = 0$

Thus, the general solution of the normal mode is given by:

$q(t) = q_0 + \sum_i c_i v_i \cos(\omega_i t + \phi_i)$

0.8 Hamiltonian Mechanics

Given a system of particles with generalized coordinates q_i , and the Lagrangian of the system, the generalised momentum p_i of the system is given by:

$p_i = \frac{\partial L}{\partial \dot{q}_i}$

And we can solve this implicit equation to get $\dot{q}_i$ in terms of q_i and p_i .

The Hamiltonian of the system is given by:

$H = p \cdot \dot{q}(q,p,t) - L(q,\dot{q}(q,p,t),t)$

0.8.1 Hamilton's Canonical Equations

By the Euler-Lagrange equation, we can derive the following equations:

$\begin{align} \frac{dH}{dp} &= \dot{q} + p \cdot \frac{d\dot{q}}{p} - \frac{dL}{d\dot{q}}\cdot \frac{d\dot{q}}{p} \\ &= \dot{q} + p \cdot \frac{d\dot{q}}{p} - p \frac{d\dot{q}}{p} \\ &= \dot{q} \end{align}$ $\begin{align} \frac{dH}{dq} &= \frac{dp}{dq} \cdot \dot{q} + p \cdot \frac{d\dot{q}}{dq} - \frac{dL}{dq} - \frac{dL}{d\dot{q}}\frac{d\dot{q}}{dq}\\ &= \frac{dp}{dq} \cdot \dot{q} + p \cdot \frac{d\dot{q}}{dq} - \dot{p} -p \frac{d\dot{q}}{dq}\\ &= -\dot{p} \end{align}$

0.8.2 Quadratic Hamiltonian

Given a system of particles with generalized coordinates q_i , if the potential energy is independent of $\dot{q}$ , and the kinetic energy of the system is quadratic in the generalized velocities $\dot{q}_i$ , which means there is a positive definite symmetric matrix M = M(q,t) such that:

$T = \frac{1}{2}\dot{q}^T M \dot{q}$

Then the Hamiltonian of the system is given by:

$\begin{align} H &= p \cdot \dot{q} - L \\ &= \frac{\partial L}{\partial\dot{q}} \cdot \dot{q} - T + U \\ &= \frac{\partial T}{\partial\dot{q}} \cdot \dot{q} - T + U \\ &= (M\dot{q}) \cdot \dot{q} -T + U \\ &= T + U \\ \end{align}$

0.8.3 Example: Harmonic Oscillator

Given a object with mass , spring constant , and displacement .

The momentum of the object is given by:

$p = \frac{\partial L}{\partial \dot{x}} = m\dot{x}$

Thus,

$\dot{x} = \frac{p}{m}$

The potential energy of the object is given by:

$U = \frac{1}{2}kx^2$

The kinetic energy of the object is given by:

$T = \frac{1}{2}m\dot{x}^2 = \frac{1}{2}m\left(\frac{p}{m}\right)^2 = \frac{p^2}{2m}$

As the potential energy is independent of $\dot{x}$ , and the kinetic energy is quadratic in $\dot{x}$ , the Hamiltonian of the object is given by:

$H = T + U = \frac{p^2}{2m} + \frac{1}{2}kx^2$

By Hamilton's canonical equations, we can determine the equation of motion of the object.

$\begin{align} \frac{\partial H}{\partial p} &= \dot{x} = \frac{p}{m} \\ \frac{\partial H}{\partial x} &= -\dot{p} \\ kx &= -\dot{p} \\ m\ddot{x} &= -kx \end{align}$

0.8.4 Cyclical Coordinates in Hamiltonian Mechanics

Given a system of particles with generalized coordinates q_i .

If the Hamiltonian does not depend on a generalized coordinate q_i , then the generalized coordinate q_i is called a cyclical coordinate.

Thus,

$\dot{p} = -\frac{\partial H}{\partial q_i} = 0$

The momentum p_i is conserved.

If the Hamiltonian does not depend on a momentum p_i , then the momentum p_i is called a cyclical momentum.

Thus,

$\dot{q} = \frac{\partial H}{\partial p_i} = 0$

The generalized coordinate q_i is conserved.

0.8.5 Example: Particle on a Cone

Consider the following system:

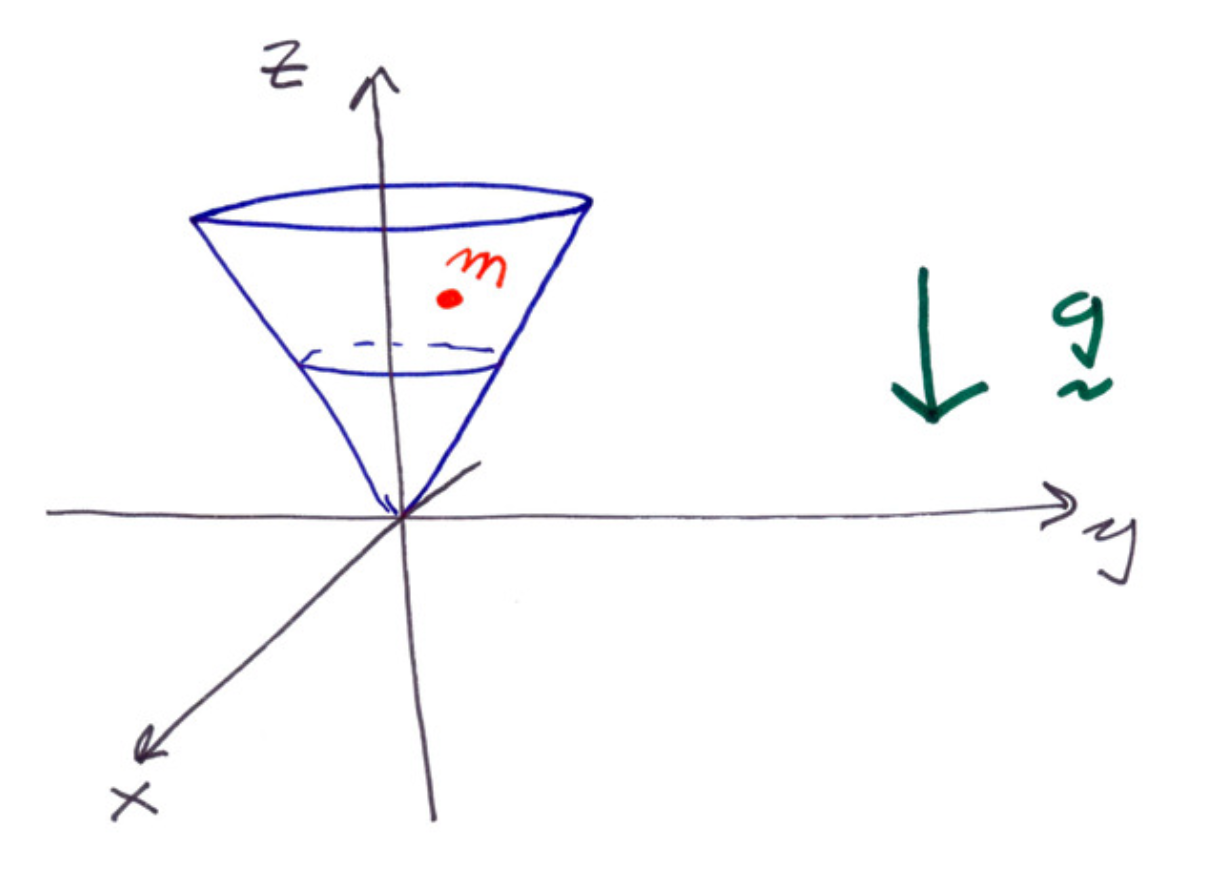
Particle on a Cone

The cone is given by:

$z = \sqrt{x^2 + y^2}$

The mass of the particle is , the cone is smooth.

Consider the following generalized coordinates:

$\begin{align} z &= z \\ \end{align}$

And $\varphi$ be the angle of the projection of the particle on the plane with the axis.

Then,

$\begin{align} x &= z\cos(\varphi) \\ y &= z\sin(\varphi) \\ z &= z \end{align}$

The kinetic energy of the particle is given by:

$\begin{align} T &= \frac{1}{2}m(\dot{x}^2 + \dot{y}^2 + \dot{z}^2) \\ &= \frac{1}{2}m(z^2\dot{\varphi}^2 + \dot{z}^2 + \dot{z}^2) \\ &= \frac{1}{2}m(2\dot{z}^2 + z^2\dot{\varphi}^2) \end{align}$

The potential energy of the particle is given by:

Thus, the Lagrangian of the particle is given by:

$L = T - U = \frac{1}{2}m(2\dot{z}^2 + z^2\dot{\varphi}^2) - mgz$

The momentum of the particle is given by:

$\begin{align} p_{z} &= \frac{\partial L}{\partial \dot{z}} = 2m\dot{z} \\ p_{\varphi} &= \frac{\partial L}{\partial \dot{\varphi}} = mz^2\dot{\varphi} \end{align}$

Thus,

$\begin{align} \dot{z} &= \frac{p_z}{2m} \\ \dot{\varphi} &= \frac{p_{\varphi}}{mz^2} \end{align}$

The Hamiltonian of the particle is given by:

$\begin{align} H &= p \cdot \dot{q} - L \\ &= p_z\dot{z} + p_{\varphi}\dot{\varphi} - L \\ &= p_z\frac{p_z}{2m} + p_{\varphi}\frac{p_{\varphi}}{mz^2} - \frac{1}{2}m(2\dot{z}^2 + z^2\dot{\varphi}^2) + mgz \\ &= \frac{p_z^2}{2m} + \frac{p_{\varphi}^2}{mz^2} - \frac{1}{2}m\left(2\left(\frac{p_z}{2m}\right)^2 + z^2\left(\frac{p_{\varphi}}{mz^2}\right)^2\right) + mgz \\ &= \frac{p_z^2}{2m} + \frac{p_{\varphi}^2}{mz^2} - \frac{p_z^2}{4m} - \frac{p_{\varphi}^2}{2mz^2} + mgz \\ &= \frac{p_z^2}{4m} + \frac{p_{\varphi}^2}{2mz^2} + mgz \end{align}$

As the Hamiltonian does not depend on the generalized coordinate $\varphi$ , the generalized coordinate $\varphi$ is a cyclical coordinate. And the momentum $p_{\varphi}$ is a constant.

Thus,

$\begin{align} \frac{dH}{dp_{\phi}} &= \dot{\varphi} \\ \frac{p_{\phi}}{mz^2} &= \dot{\varphi} \\ \end{align}$

For coordinate,

$\begin{align} \frac{dH}{dp_{z}} &= \dot{z} \\ \frac{p_{z}}{2m} &= \dot{z} \\ \end{align}$

If we are given the initial energy of the particle , then the Hamiltonian of the particle is given by:

$\begin{align} E &= \frac{p_z^2}{4m} + \frac{p_{\varphi}^2}{2mz^2} + mgz \\ &= m\dot{z}^2 + \frac{p_{\varphi}^2}{2mz^2} + mgz \end{align}$

Which became a first order separable ODE in .

If $p_{\varphi} = 0$ , then the particle is moving vertically just like sliding on a smooth surface.

If $p_{\varphi} \neq 0$ , then the term $\frac{p_{\varphi}^2}{2mz^2} + mgz$ has lowest energy at $z_0 = \sqrt[3]{\frac{p_{\varphi}}{m^2g}}$ with energy E_0 .

If E = E_0 , then $m\dot{z}^2 = 0$ , and the particle is doing a circular motion on the cone.

If E > E_0 , then the particle is doing oscillatory motion on the cone. By using Taylor expansion of $\frac{p_{\varphi}^2}{2mz^2} + mgz$ around z_0 , We could derive:

$m\dot{z}^2 + E_0 + \frac{1}{2}\left.(\frac{p_{\varphi}^2}{2mz^2} + mgz)''\right|_{z_{0}} (z-z_0)^2 \approx E$

And we could expect the angular frequency of the oscillatory motion to be approximately:

$\omega = \sqrt{\frac{1}{2m}\left.(\frac{p_{\varphi}^2}{2mz^2} + mgz)''\right|_{z_{0}}}$

0.8.6 Phase Space

Given a system of particles with generalized coordinates q_i , and the Hamiltonian of the system, the phase space $\Gamma$ of the system is the space of generalized coordinates q_i and momenta p_i .

The phase space of the system is a dimensional space, where is the number of generalized coordinates q_i .

0.8.6.1 Hamiltonian Flow

The trajectory of the system together with the change of the momentum of the system, generate a path in in the phase space of the system, and the Hamiltonian canonical equations describe the flow of the system in the phase space.

$\begin{align} \frac{dq_i}{dt} &= \frac{\partial H}{\partial p_i} \\ \frac{dp_i}{dt} &= -\frac{\partial H}{\partial q_i} \end{align}$

0.8.6.2 Liouville's Theorem

Given a system of particles with generalized coordinates q_i , and the Hamiltonian of the system, the volume of the phase space of the system is conserved. In other words, the Hamiltonian flow of the system is incompressible.

$\frac{dV}{dt} = 0$

0.8.6.3 Phase Space Portrait

Given a system of particles with generalized coordinates q_i , and the Hamiltonian of the system, the phase space portrait of the system is the plot of the trajectory of the system in the phase space of the system.

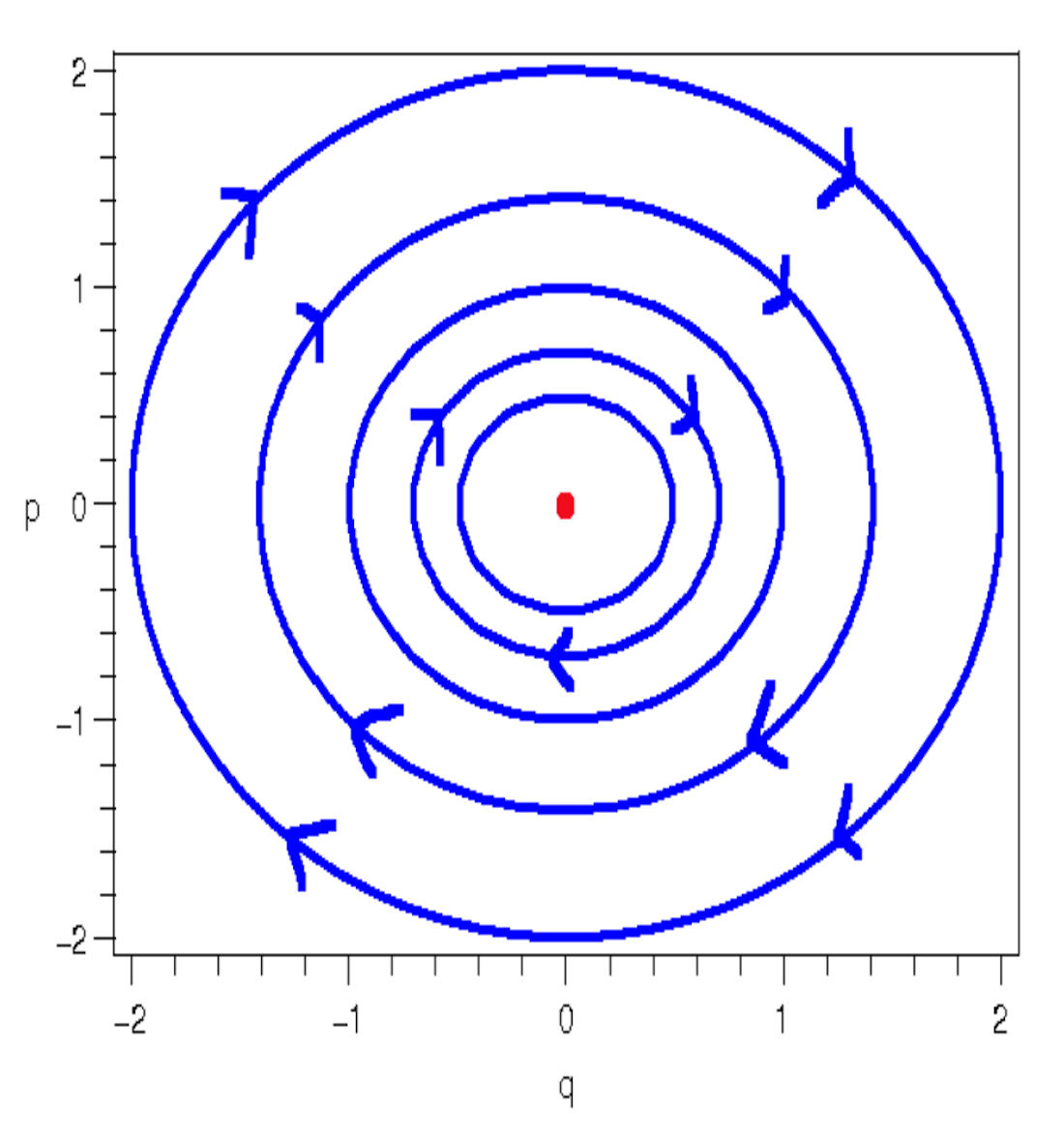
0.8.6.3.1 Example: Phase Space Portrait of a Harmonic Oscillator

Given a object with mass , spring constant , and displacement . The Hamiltonian of the object is given by:

$H = \frac{p^2}{2m} + \frac{1}{2}kx^2$

The Phase Space Portrait of the object is like:

Phase Space Portrait of a Harmonic Oscillator

0.8.7 Poisson Brackets

Given a system of particles with generalized coordinates q_i , and the Hamiltonian of the system, the Poisson bracket of two functions and of the phase space of the system is given by:

$\{f,g\} = \sum_i \left(\frac{\partial f}{\partial q_i}\frac{\partial g}{\partial p_i} - \frac{\partial f}{\partial p_i}\frac{\partial g}{\partial q_i}\right)$

0.8.7.1 Properties of Poisson Brackets

Given a system of particles with generalized coordinates q_i , and the Hamiltonian of the system, the Poisson bracket of two functions and of the phase space of the system has the following properties:

Antisymmetry: $\{f,g\} = -\{g,f\}$
Linearity: $\{af + bg, h\} = a\{f,h\} + b\{g,h\}$
Product(Leibnitz) Rule: $\{fg,h\} = f\{g,h\} + g\{f,h\}$

0.8.7.2 Fundamental Poisson Brackets

Given a system of particles with generalized coordinates q_i , and the Hamiltonian of the system, the fundamental Poisson brackets of the system are given by:

$\begin{align} \{q_i,p_j\} &= \delta_{ij} \\ \{q_i,q_j\} &= 0 \\ \{p_i,p_j\} &= 0 \end{align}$

0.8.7.3 Constant of Motion and Poisson Brackets

Given a system of particles with generalized coordinates q_i , and the Hamiltonian of the system, and a function of the phase space of the system, then time derivative of the function is given by:

$\begin{align} \frac{df}{dt} &= \{f,H\} + \frac{\partial f}{\partial t} \end{align}$

Thus, if the function is independent of time, then the function is a constant of motion.

←Previous Post Next Post→

7 Days	0	Site 7 Days	0
30 Days	0	Site 30 Days	0
Total	0	Site Total	0